An explanation of machine learning models even you could understand

If you are new to data science, this title is not intended to insult you. It is my second post on the theme of a popular interview question that goes something like: “explain [insert technical topic] to me as though I were a five-year-old.”

Turns out, hitting the five-year-old comprehension level is pretty tough. So, while this article may not be perfectly clear to a kindergartener, it should be clear to someone with little to no background in data science (and if it isn’t by the end, please let me know in the comments).

I will start out by explaining what machine learning is, along with the different types of machine learning, and then I will jump into explaining common models. I won’t go into any of the math, but I am considering doing that in another article in the future. Enjoy!

Definition of machine learning

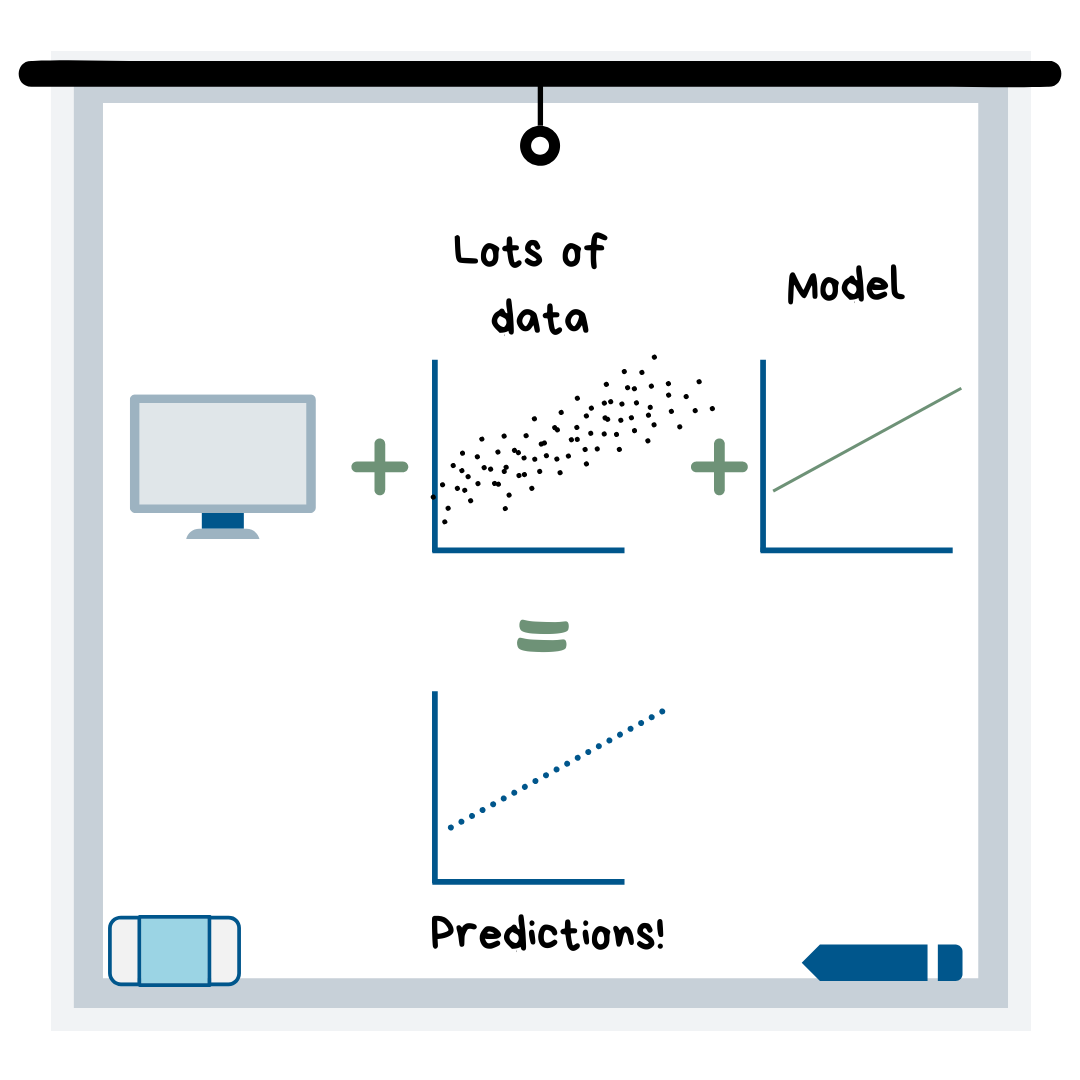
Machine learning is when you load lots of data into a computer program and choose a model to “fit” the data, which allows the computer (without your help) to come up with predictions. The way the computer makes the model is through algorithms, which can range from a simple equation (like the equation of a line) to a very complex system of logic/math that gets the computer to the best predictions.

Read: [The difference between AI and machine learning, explained]

Machine learning is aptly named, because once you choose the model to use and tune it (a.k.a. improve it through adjustments), the machine will use the model to learn the patterns in your data. Then, you can input new conditions (observations) and it will predict the outcome!

Definition of supervised machine learning

Supervised learning is a type of machine learning where the data you put into the model is “labeled.” Labeled simply means that the outcome of the observation (a.k.a. the row of data) is known. For example, if your model is trying to predict whether your friends will go golfing or not, you might have variables like the temperature, the day of the week, etc. If your data is labeled, you would also have a variable that has a value of 1 if your friends actually went golfing or 0 if they did not.

Definition of unsupervised machine learning

As you may have guessed, unsupervised learning is the opposite of supervised learning when it comes to labeled data. With unsupervised learning, you do not know whether your friends went golfing or not — it is up to the computer to find patterns via a model to guess what happened or predict what will happen.

Supervised machine learning models

Logistic Regression

Logistic regression is used when you have a classification problem. This means that your target variable (a.k.a. the variable you are interested in predicting) is made up of categories. These categories could be yes/no, or something like a number between 1 and 10 representing customer satisfaction.

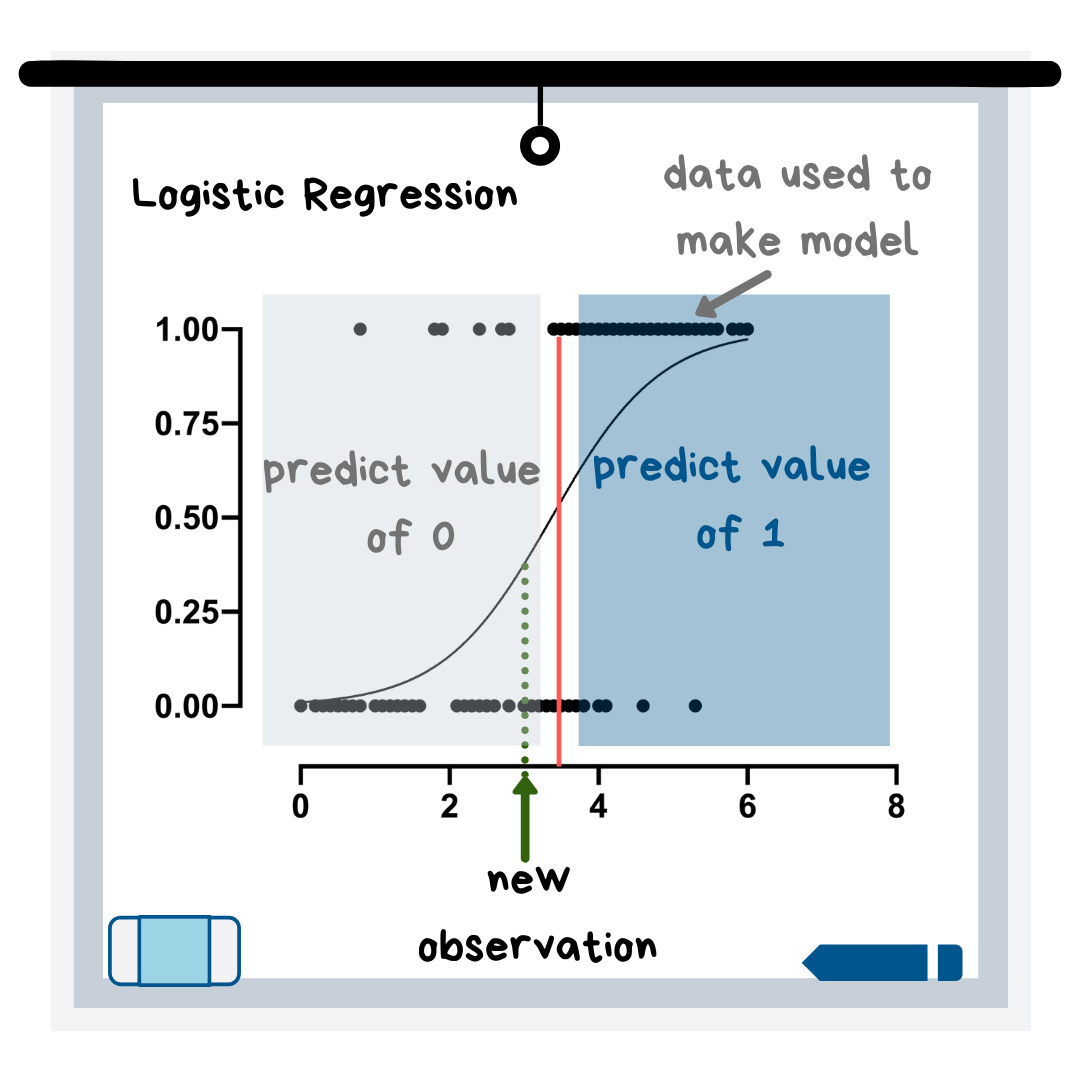
The logistic regression model uses an equation to create a curve with your data and then uses this curve to predict the outcome of a new observation.

In the graphic above, the new observation would get a prediction of 0 because it falls on the left side of the curve. If you look at the data this curve is based on, it makes sense because, in the “predict a value of 0” region of the graph, the majority of the data points have a y-value of 0.

Linear Regression

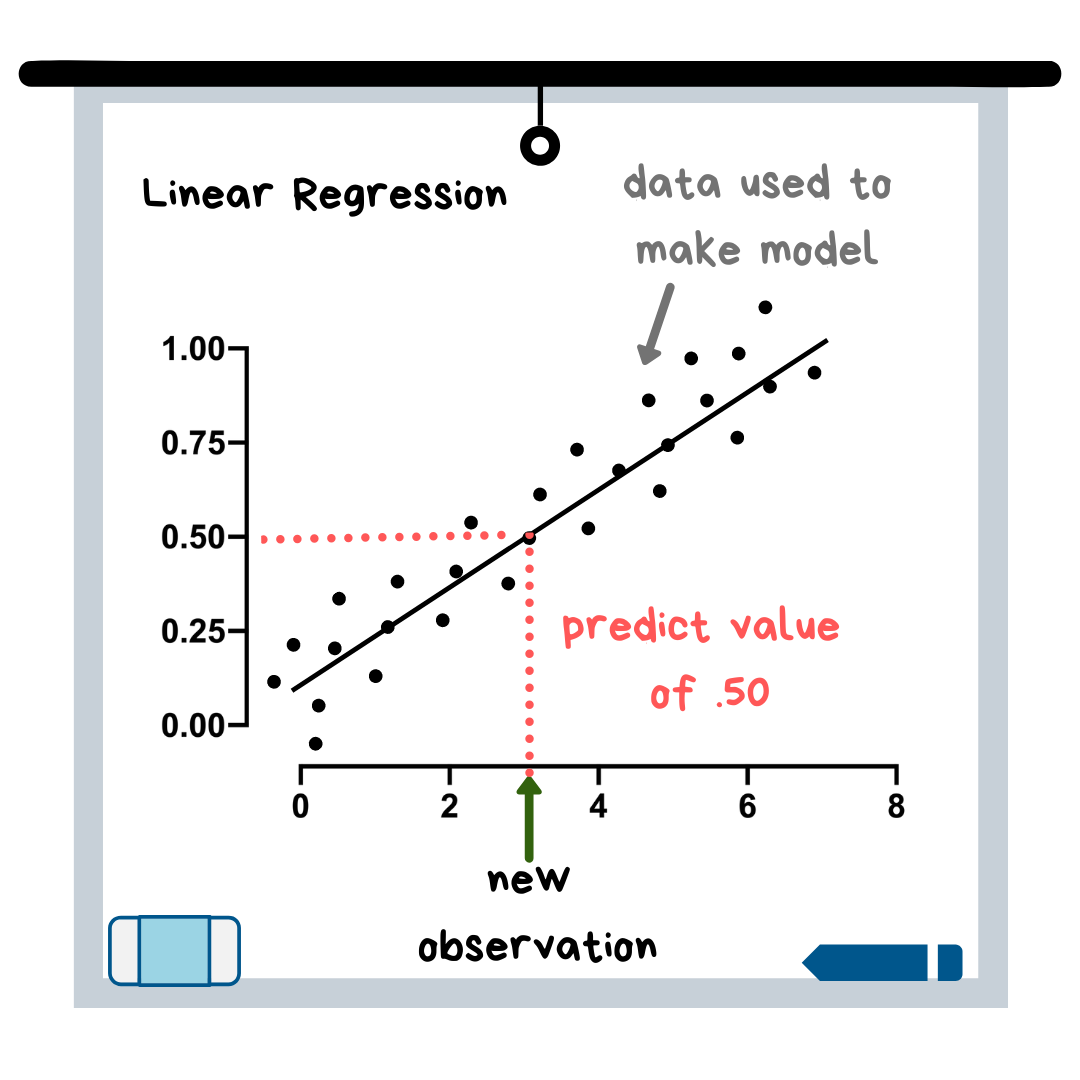
Linear regression is often one of the first machine learning models that people learn. This is because its algorithm (i.e. the equation behind the scenes) is relatively easy to understand when using just one x-variable — it is just making a best-fit line, a concept taught in elementary school. This best-fit line is then used to make predictions about new data points (see illustration).

Linear Regression is similar to logistic regression, but it is used when your target variable is continuous, which means it can take on essentially any numerical value. In fact, any model with a continuous target variable can be categorized as “regression.” An example of a continuous variable would be the selling price of a house.

Linear regression is also very interpretable. The model equation contains coefficients for each variable, and these coefficients indicate how much the target variable changes for each small change in the independent variable (the x-variable). With the house prices example, this means that you could look at your regression equation and say something like “oh, this tells me that for every increase in 1ft² of house size (the x-variable), the selling price (the target variable) increases by $25.”

K Nearest Neighbors (KNN)

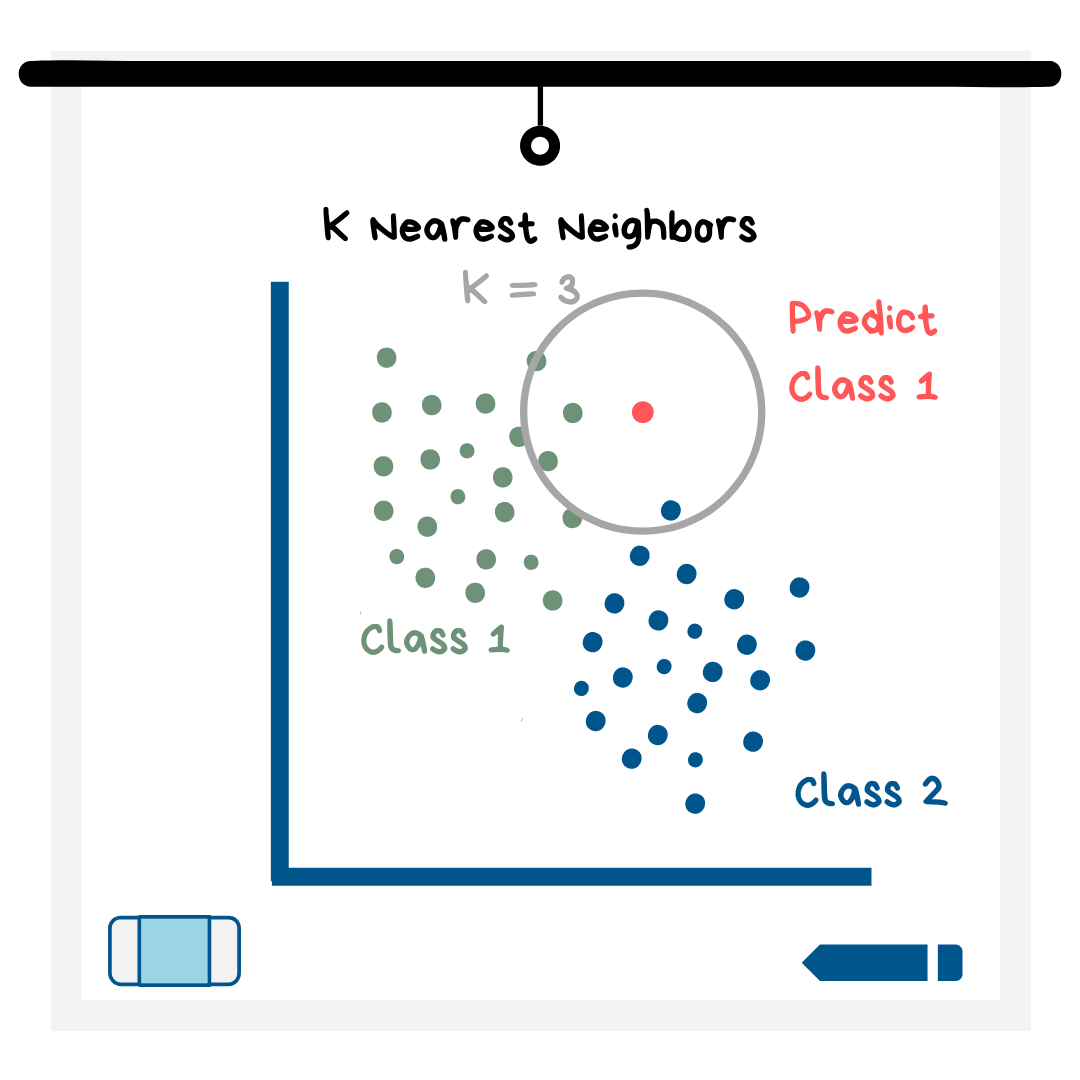
This model can be used for either classification or regression! The name “K Nearest Neighbors” is not intended to be confusing. The model first plots out all of the data. The “K” part of the title refers to the number of closest neighboring data points that the model looks at to determine what the prediction value should be (see illustration below). You, as the future data scientist, get to choose K and you can play around with the values to see which one gives the best predictions.

All of the data points that are in the K=__ circle get a “vote” on what the target variable value should be for this new data point. Whichever value receives the most votes is the value that KNN predicts for the new data point. In the illustration above, 2 of the nearest neighbors are class 1, while 1 of the neighbors is class 2. Thus, the model would predict class 1 for this data point. If the model is trying to predict a numerical value instead of a category, then all of the “votes” are numerical values that are averaged to get a prediction.

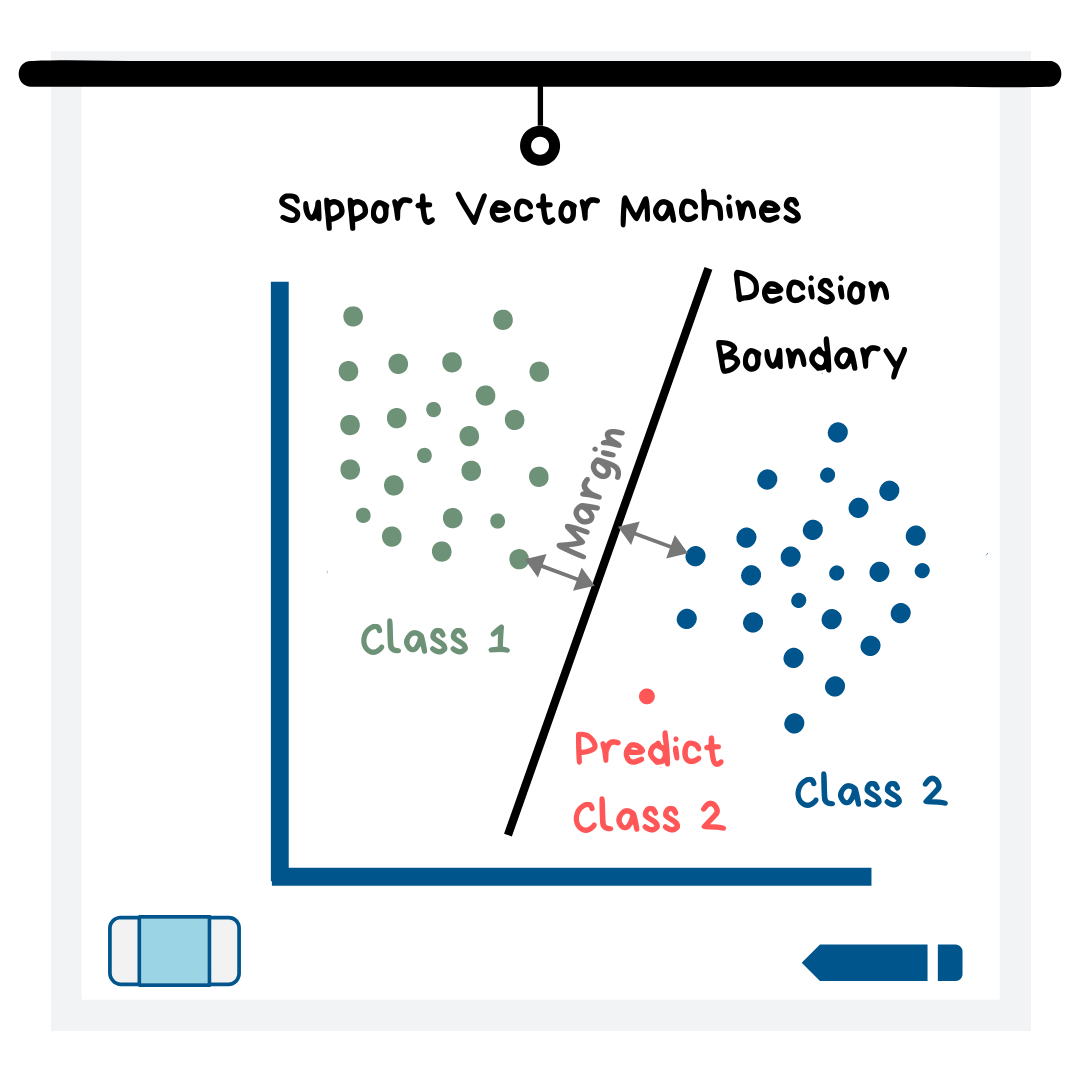
Support Vector Machines (SVMs)

Support Vector Machines work by establishing a boundary between data points, where the majority of one class falls on one side of the boundary (a.k.a. line in the 2D case) and the majority of the other class falls on the other side.

The way it works is the machine seeks to find the boundary with the largest margin. The margin is defined as the distance between the nearest point of each class and the boundary (see illustration). New data points are then plotted and put into a class depending on which side of the boundary they fall on.

My explanation of this model is for the classification case, but you can also use SVMs for regression!

Decision trees & random forests

I already explained these in a previous article — check it out here (decision trees and random forests are near the end).

Unsupervised machine learning models

[Use with discretion]

Now we are venturing into unsupervised learning (a.k.a. the deep end, pun intended). As a reminder, this means that our data set is not labeled, so we do not know the outcomes of our observations.

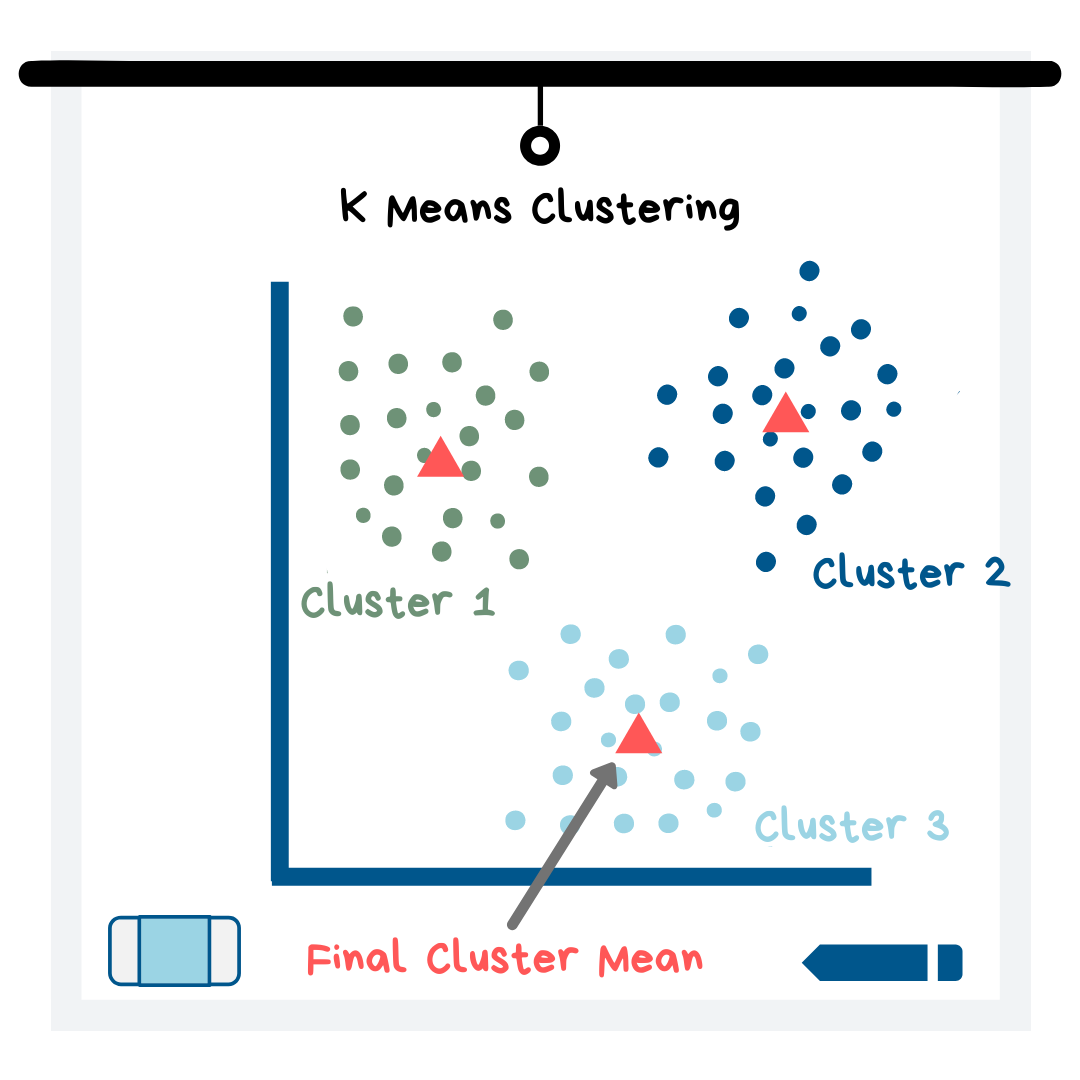
K Means Clustering

When you use K means clustering, you have to start by assuming there are K clusters in your dataset. Since you do not know how many groups there really are in your data, you have to try out different K values and use visualizations and metrics to see which value of K makes sense. K means works best with clusters that are circular and of similar size.

The K Means algorithm first chooses the best K data points to form the center of each of the K clusters. Then, it repeats the following two steps for every point:

Assign a data point to the nearest cluster center

Create a new center by taking the mean of all of the data points that are now in this cluster

DBSCAN Clustering

The DBSCAN clustering model differs from K means in that it does not require you to input a value for K, and it also can find clusters of any shape (see illustration below). Instead of specifying the number of clusters, you input the minimum number of data points you want in a cluster and the radius around a data point to search for a cluster. DBSCAN will find the clusters for you! Then you can change the values used to make the model until you get clusters that make sense for your dataset.

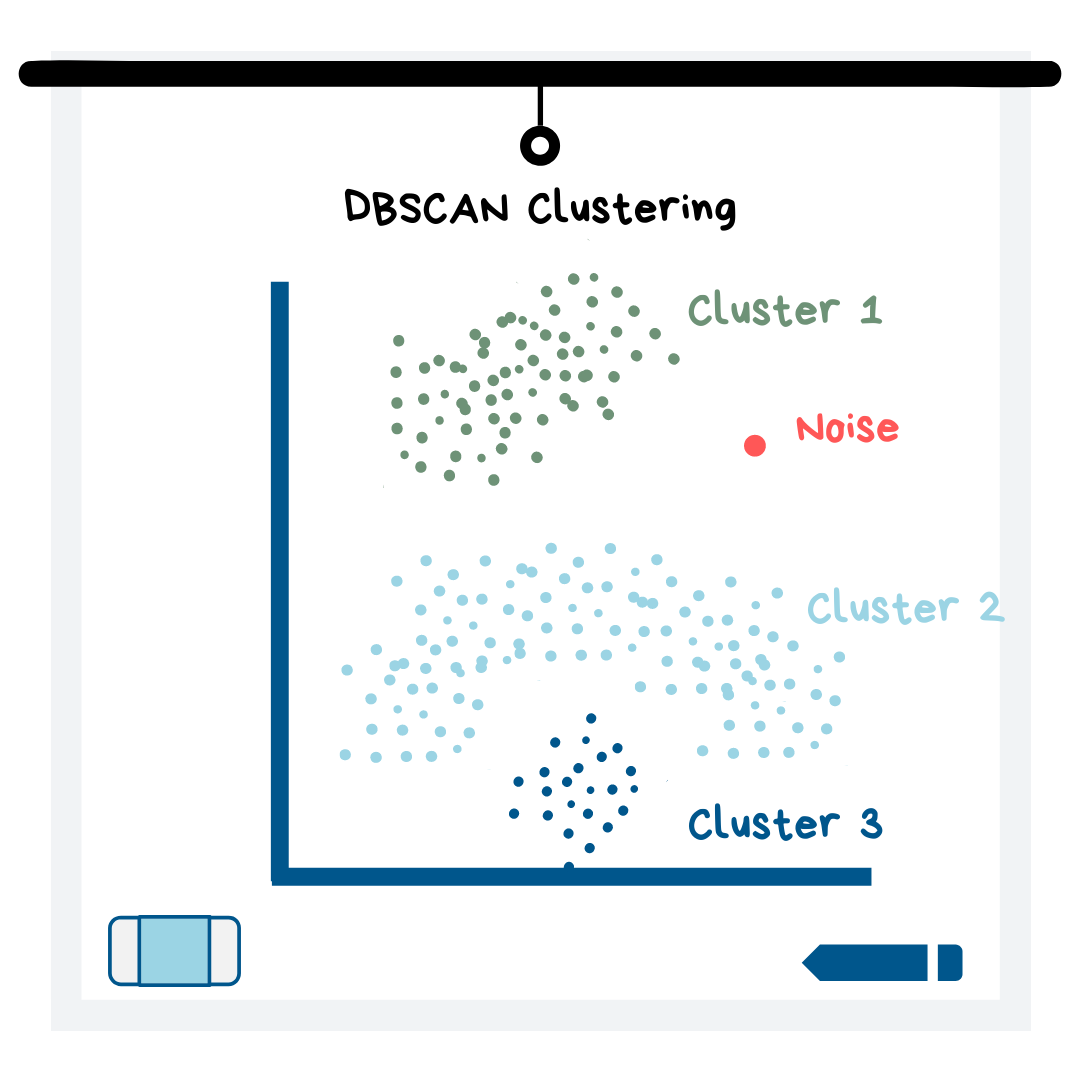
Additionally, the DBSCAN model classifies “noise” points for you (i.e. points that are far away from all other observations). This model works better than K means when data points are very close together.

Neural networks

Neural networks are the coolest and most mysterious models, in my opinion. They are called neural networks because they are modeled after how the neurons in our brains work. These models work to find patterns in the dataset; sometimes they find patterns that humans might never recognize.

Neural networks work well with complex data like images and audio. They are behind lots of software functionality that we see all the time these days, from facial recognition (stop being creepy, Facebook) to text classification. Neural networks can be used with data that is labeled (i.e. supervised learning applications) or data that is unlabeled (unsupervised learning) as well.

Even just touching the surface of how neural networks operate would likely be too complex for this article. If you would like to learn more, here is a “beginner’s” guide: https://pathmind.com/wiki/neural-network.

Hopefully, this article has not only increased your understanding of these models but also made you realize how cool and useful they are! When we let the computer do the work/learning, we get to sit back and see what patterns it finds. Sometimes it can be confusing because even the experts do not understand the logic of exactly why the computer came to the conclusion it did, but in some cases, all we care about is that it’s good at predicting.

However, there are times when we do care how the computer got to its prediction, like if we are using the model to determine which job candidates will get first-round interviews.

This article was originally published on Towards Data Science by Megan Dibble, an Industrial Engineer turned Data Scientist.